Gleichung
Unter einer Gleichung versteht man in der Mathematik eine Aussage über die Gleichheit zweier Terme, die mit Hilfe des Gleichheitszeichens („=“) symbolisiert wird. Formal hat eine Gleichung die Gestalt
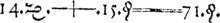
- ,
wobei der Term die linke Seite und der Term die rechte Seite der Gleichung genannt wird. Gleichungen sind entweder wahr beziehungsweise erfüllt (beispielsweise ) oder falsch (beispielsweise ). Wenn zumindest einer der Terme von Variablen abhängig ist, liegt nur eine Aussageform vor; ob die Gleichung wahr oder falsch ist, hängt dann von den konkreten eingesetzten Werten ab. Die Werte der Variablen, für die die Gleichung erfüllt ist, heißen Lösungen der Gleichung. Liegen zwei oder mehr Gleichungen vor, spricht man auch von einem Gleichungssystem. Die Lösung eines Gleichungssystems muss alle Gleichungen gleichzeitig erfüllen.
Typen von Gleichungen
BearbeitenGleichungen werden in vielen Zusammenhängen verwendet; dementsprechend gibt es verschiedene Möglichkeiten, die Gleichungen nach unterschiedlichen Gesichtspunkten einzuteilen. Die jeweiligen Einteilungen sind zu einem großen Teil unabhängig voneinander, eine Gleichung kann in mehrere dieser Gruppen fallen. So ist es etwa sinnvoll, von einem System linearer partieller Differentialgleichungen zu sprechen.
Einteilung nach Gültigkeit
BearbeitenIdentitätsgleichungen
BearbeitenGleichungen können allgemeingültig sein, also durch Einsetzen aller Variablenwerte aus einer gegebenen Grundmenge oder zumindest aus einer vorher definierten Teilmenge davon wahr sein. Solche Gleichungen werden als Identitätsgleichungen oder Identitäten bezeichnet. Die Allgemeingültigkeit kann entweder aus anderen Axiomen gefolgert werden oder selber als Axiom vorausgesetzt werden.
Beispiele sind:
- Der Satz des Pythagoras: ist wahr für rechtwinklige Dreiecke, falls die dem rechten Winkel gegenüberliegende Seite (Hypotenuse) und die Katheten bezeichnen.
- Das Assoziativgesetz: ist wahr für alle natürlichen Zahlen und allgemein für beliebige Elemente einer Gruppe (als Axiom).
- Die erste binomische Formel: ist wahr für alle reellen Zahlen .
- Die eulersche Identität: ist wahr für alle reellen .
In diesem Zusammenhang spricht man auch von einem mathematischen Satz oder Gesetz. Zur Unterscheidung von nicht-allgemeingültigen Gleichungen wird bei Identitäten statt des Gleichheitszeichens auch das Kongruenzzeichen („≡“) verwendet.
Bestimmungsgleichungen
BearbeitenHäufig besteht eine Aufgabenstellung darin, alle Variablenbelegungen zu bestimmen, für die die Gleichung wahr wird. Diesen Vorgang bezeichnet man als Lösen der Gleichung. Zur Unterscheidung von Identitätsgleichungen werden solche Gleichungen als Bestimmungsgleichungen bezeichnet.[2] Die Menge der Variablenbelegungen, für die die Gleichung wahr ist, bezeichnet man als Lösungsmenge der Gleichung. Wenn es sich bei der Lösungsmenge um die leere Menge handelt, so bezeichnet man die Gleichung als unlösbar oder unerfüllbar.
Ob eine Gleichung lösbar ist oder nicht, kann von der betrachteten Grundmenge abhängen, zum Beispiel gilt:
- Die Gleichung ist unlösbar als Gleichung über den natürlichen oder den rationalen Zahlen und besitzt die Lösungsmenge als Gleichung über den reellen Zahlen.
- Die Gleichung ist unlösbar als Gleichung über den reellen Zahlen und besitzt die Lösungsmenge als Gleichung über den komplexen Zahlen.
Bei Bestimmungsgleichungen treten mitunter Variablen auf, die nicht gesucht sind, sondern als bekannt vorausgesetzt werden. Solche Variablen werden als Parameter bezeichnet. Beispielsweise lautet die Lösungsformel für die quadratische Gleichung
bei gesuchter Unbekannte und gegebenen Parametern und
- .
Setzt man eine der beiden Lösungen in die Gleichung ein, so verwandelt sich die Gleichung in eine Identität, wird also für eine beliebige Wahl von und zur wahren Aussage. Für sind hier die Lösungen reell, ansonsten komplex.
Definitionsgleichungen
BearbeitenGleichungen können auch verwendet werden, um ein neues Symbol zu definieren. In diesem Fall wird das zu definierende Symbol links geschrieben, und das Gleichheitszeichen oft durch das Definitionszeichen („:=“) ersetzt oder über das Gleichheitszeichen „def“ geschrieben.
Zum Beispiel wird die Ableitung einer Funktion an einer Stelle durch
definiert. Im Gegensatz zu Identitäten sind Definitionen keine Aussagen; sie sind also weder wahr noch falsch, sondern nur mehr oder weniger zweckmäßig.
Einteilung nach rechter Seite
BearbeitenHomogene Gleichungen
BearbeitenEine Bestimmungsgleichung der Form
heißt homogene Gleichung. Ist eine Funktion, nennt man die Lösung auch Nullstelle der Funktion. Homogene Gleichungen spielen bei der Lösungsstruktur linearer Gleichungssysteme und linearer Differentialgleichungen eine wichtige Rolle. Ist die rechte Seite einer Gleichung ungleich Null, heißt die Gleichung inhomogen.
Fixpunktgleichungen
BearbeitenEine Bestimmungsgleichung der Form
heißt Fixpunktgleichung und deren Lösung nennt man Fixpunkt der Gleichung. Genaueres über die Lösungen solcher Gleichungen sagen Fixpunktsätze aus.
Eigenwertprobleme
BearbeitenEine Bestimmungsgleichung der Form
heißt Eigenwertproblem, wobei die Konstante (der Eigenwert) und die Unbekannte (der Eigenvektor) gemeinsam gesucht werden. Eigenwertprobleme besitzen vielfältige Einsatzbereiche in der linearen Algebra, beispielsweise bei der Analyse und Zerlegung von Matrizen, und in Anwendungsgebieten, beispielsweise der Strukturmechanik und der Quantenmechanik.
Einteilung nach Linearität
BearbeitenLineare Gleichungen
BearbeitenEine Gleichung heißt linear, wenn sie in die Form
gebracht werden kann, wobei der Term unabhängig von ist und der Term linear in ist, also
für Koeffizienten gilt. Sinnvollerweise müssen die passenden Operationen definiert sein, es ist also notwendig, dass und aus einem Vektorraum sind, und die Lösung aus dem gleichen oder einem anderen Vektorraum gesucht wird.
Lineare Gleichungen sind normalerweise wesentlich einfacher zu lösen als nichtlineare. So gilt für lineare Gleichungen das Superpositionsprinzip: Die allgemeine Lösung einer inhomogenen Gleichung ist die Summe einer Partikulärlösung der inhomogenen Gleichung und der allgemeinen Lösung der zugehörigen homogenen Gleichung.
Wegen der Linearität ist zumindest eine Lösung einer homogenen Gleichung. Hat eine homogene Gleichung also eine eindeutige Lösung, so hat auch eine entsprechende inhomogene Gleichung höchstens eine Lösung. Eine verwandte, aber wesentlich tiefer gehende Aussage in der Funktionalanalysis ist die Fredholmsche Alternative.
Nichtlineare Gleichungen
BearbeitenNichtlineare Gleichungen werden oft nach der Art der Nichtlinearität unterschieden. Insbesondere in der Schulmathematik werden die nachfolgenden Grundtypen von nichtlinearen Gleichungen behandelt.[3]
Algebraische Gleichungen
BearbeitenHandelt es sich bei dem Gleichungsterm um ein Polynom, spricht man von einer algebraischen Gleichung. Ist dabei das Polynom mindestens vom Grad zwei, so bezeichnet man die Gleichung als nichtlinear. Beispiele sind allgemeine quadratische Gleichungen der Form
oder kubische Gleichungen der Form
- .
Für Polynomgleichungen bis zum Grad vier gibt es allgemeine Lösungsformeln.
Bruchgleichungen
BearbeitenEnthält eine Gleichung einen Bruchterm, bei dem die Unbekannte zumindest im Nenner vorkommt, spricht man von einer Bruchgleichung, zum Beispiel
- .
Durch Multiplikation mit dem Hauptnenner, im Beispiel , lassen sich Bruchgleichungen auf algebraische Gleichungen zurückführen. Eine solche Multiplikation ist im Regelfall keine Äquivalenzumformung und es muss eine Fallunterscheidung vorgenommen werden, im Beispiel ist nicht im Definitionsbereich der Bruchgleichung enthalten.
Wurzelgleichungen
BearbeitenBei Wurzelgleichungen steht die Unbekannte mindestens einmal unter einer Wurzel, beispielsweise
Wurzelgleichungen sind spezielle Potenzgleichungen mit Exponent . Wurzelgleichungen lassen sich lösen, indem eine Wurzel isoliert wird und dann die Gleichung mit dem Wurzelexponenten (im Beispiel ist ) potenziert wird. Dieses Vorgehen wird wiederholt, bis alle Wurzeln eliminiert sind. Potenzieren mit geradzahligem Exponenten stellt keine Äquivalenzumformung dar und daher ist in diesen Fällen bei der Ermittlung der Lösung eine entsprechende Fallunterscheidung vorzunehmen. Im Beispiel führt Quadrieren zu der quadratischen Gleichung , deren negative Lösung nicht im Definitionsbereich der Ausgangsgleichung liegt.
Exponentialgleichungen
BearbeitenBei Exponentialgleichungen steht die Unbekannte mindestens einmal im Exponenten, zum Beispiel:
Exponentialgleichungen lassen sich durch Logarithmieren lösen. Umgekehrt sind Logarithmusgleichungen - also Gleichungen, bei denen die Unbekannte als Numerus (Argument einer Logarithmusfunktion) auftritt - durch Exponenzieren lösbar.
Trigonometrische Gleichungen
BearbeitenTreten die Unbekannten als Argument mindestens einer Winkelfunktion auf, so spricht man von einer trigonometrischen Gleichung, beispielsweise
Die Lösungen trigonometrischer Gleichungen wiederholen sich im Allgemeinen periodisch, sofern die Lösungsmenge nicht auf ein bestimmtes Intervall, etwa , beschränkt wird. Alternativ können die Lösungen durch eine ganzzahlige Variable parametrisiert werden. Beispielsweise sind die Lösungen obiger Gleichung gegeben als
- mit .
Einteilung nach gesuchten Unbekannten
BearbeitenAlgebraische Gleichungen
BearbeitenUm Gleichungen, bei denen eine reelle Zahl oder ein reeller Vektor gesucht wird, von Gleichungen, bei denen beispielsweise eine Funktion gesucht ist, zu unterscheiden, wird manchmal auch die Bezeichnung algebraische Gleichung verwendet, wobei diese Bezeichnung dann aber nicht auf Polynome eingeschränkt ist. Diese Sprechweise ist jedoch umstritten.
Diophantische Gleichungen
BearbeitenSucht man ganzzahlige Lösungen einer skalaren Gleichung mit ganzzahligen Koeffizienten, so spricht man von einer Diophantischen Gleichung. Ein Beispiel einer kubischen Diophantischen Gleichung ist
- ,
von der ganzzahlige gesucht werden, die die Gleichung erfüllen, hier die Zahlen .
Differenzengleichungen
BearbeitenIst die Unbekannte eine Folge, so spricht man von einer Differenzengleichung. Ein bekanntes Beispiel einer linearen Differenzengleichung zweiter Ordnung ist
- ,
deren Lösung für Startwerte und die Fibonacci-Folge ist.
Funktionalgleichungen
BearbeitenIst die Unbekannte der Gleichung eine Funktion, die ohne Ableitungen auftritt, so spricht man von einer Funktionalgleichung. Ein Beispiel für eine Funktionalgleichung ist
- ,
deren Lösungen gerade die Exponentialfunktionen sind.
Differentialgleichungen
BearbeitenWird in der Gleichung eine Funktion gesucht, die mit Ableitungen auftritt, so spricht man von einer Differentialgleichung. Differentialgleichungen treten bei der Modellierung von naturwissenschaftlichen Problemen sehr häufig auf. Die höchste auftretende Ableitung wird dabei Ordnung der Differentialgleichung genannt. Man unterscheidet:
- gewöhnliche Differentialgleichungen, bei denen nur Ableitungen nach einer einzigen Variablen auftreten, zum Beispiel die lineare gewöhnliche Differentialgleichung erster Ordnung
- partielle Differentialgleichungen, bei denen partielle Ableitungen nach mehreren Variablen auftreten, zum Beispiel die lineare Transportgleichung erster Ordnung
- differential-algebraische Gleichungen, bei denen sowohl algebraische Gleichungen als auch Differentialgleichungen gemeinsam auftreten, beispielsweise die Euler-Lagrange-Gleichungen für ein mathematisches Pendel
- stochastische Differentialgleichungen, bei denen neben deterministischen auch stochastische Ableitungsterme vorkommen, beispielsweise die Black-Scholes-Gleichung der Finanzmathematik zur Modellierung von Wertpapierkursen
Integralgleichungen
BearbeitenTritt die gesuchte Funktion in einem Integral auf, so spricht man von einer Integralgleichung. Ein Beispiel einer linearen Integralgleichung 1. Art ist
- .
Gleichungsketten
BearbeitenBefinden sich in einer Zeile mehrere Gleichheitszeichen, so spricht man von einer Gleichungskette. In einer Gleichungskette sollen alle durch Gleichheitszeichen getrennten Ausdrücke vom Wert her gleich sein. Dabei ist jeder dieser Ausdrücke separat zu betrachten. Beispielsweise ist die Gleichungskette
falsch, weil sie in Einzelgleichungen zerlegt zu falschen Aussagen führt. Wahr ist dagegen zum Beispiel
- .
Gleichungsketten sind insbesondere wegen der Transitivität der Gleichheitsrelation sinnvoll interpretierbar. Gleichungsketten treten oft auch gemeinsam mit Ungleichungen in Abschätzungen auf, so gilt beispielsweise für
- .
Gleichungssysteme
BearbeitenOft werden mehrere Gleichungen, die gleichzeitig erfüllt sein müssen, betrachtet und dabei mehrere Unbekannte gleichzeitig gesucht.
Lineare Gleichungssysteme
BearbeitenEin Gleichungssystem – also eine Menge von Gleichungen – heißt lineares Gleichungssystem, wenn alle Gleichungen linear sind. Beispielsweise ist
ein lineares Gleichungssystem, bestehend aus zwei Gleichungen und drei Unbekannten und . Fasst man die Koeffizienten zu einer Matrix („Koeffizientenmatrix“), die Unbekannten zu einem Vektor und die Zahlen der rechten Seiten zu einem Vektor („rechte Seite“) zusammen, so lässt sich ein Gleichungssystem auch als eine einzelne Vektorgleichung
auffassen, wobei das Matrix-Vektor-Produkt ist. In obigem Beispiel sind
- , und .
Die lineare Algebra stellt effiziente Verfahren zur Lösung von linearen Gleichungssystemen bereit.
Nichtlineare Gleichungssysteme
BearbeitenGleichungssysteme, deren Gleichungen nicht alle linear sind, werden nichtlineare Gleichungssysteme genannt. Beispielsweise ist
ein nichtlineares Gleichungssystem mit den Unbekannten und . Für solche Gleichungssysteme gibt es keine allgemeingültigen Lösungsstrategien. Oftmals hat man nur die Möglichkeit, näherungsweise Lösungen mit Hilfe numerischer Verfahren zu bestimmen. Ein mächtiges Näherungsverfahren ist beispielsweise das Newton-Verfahren.
Eine Faustregel besagt, dass gleich viele Gleichungen wie Unbekannte benötigt werden, damit ein Gleichungssystem eindeutig lösbar ist. Das ist aber tatsächlich nur eine Faustregel, bis zu einem gewissen Grad gilt sie wegen des Hauptsatzes über implizite Funktionen für reelle Gleichungen mit reellen Unbekannten.
Lösen von Gleichungen
BearbeitenAnalytische Lösung
BearbeitenUnter einer analytischen Lösung versteht man eine allgemeine Umformung einer Gleichung, sodass die gesuchte Variable alleine auf einer Gleichungsseite steht und die Lösung exakt ermittelt werden kann.[4] Wichtigstes Hilfsmittel dabei sind Äquivalenzumformungen, durch die eine Gleichung schrittweise in andere äquivalente Gleichungen (die also dieselbe Lösungsmenge haben) umgeformt wird.[5] Eine analytische Lösung ist nur bei speziellen Gleichungen möglich.[4]
Numerische Lösung
BearbeitenViele Gleichungen, insbesondere aus naturwissenschaftlichen Anwendungen, können nicht analytisch gelöst werden. In diesem Fall versucht man, am Computer eine näherungsweise numerische Lösung zu berechnen. Solche Verfahren werden in der numerischen Mathematik behandelt. Viele nichtlineare Gleichungen lassen sich approximativ lösen, indem die in der Gleichung auftretenden Nichtlinearitäten linear angenähert werden, und dann die entstehenden linearen Probleme gelöst werden (beispielsweise im Newton-Verfahren). Für andere Problemklassen, etwa bei der Lösung von Gleichungen in unendlich-dimensionalen Räumen, wird die Lösung in geeignet gewählten endlich-dimensionalen Unterräumen gesucht (beispielsweise in der Galerkin-Methode).
Qualitative Analyse
BearbeitenAuch wenn eine Gleichung nicht analytisch gelöst werden kann, ist es dennoch oft möglich, mathematische Aussagen über die Lösung zu treffen. Insbesondere interessieren Fragestellungen, ob eine Lösung überhaupt existiert, ob sie eindeutig ist, und ob sie stetig von den Parametern der Gleichung abhängt. Ist dies der Fall spricht man von einem korrekt gestellten Problem. Eine qualitative Analyse ist auch bzw. gerade bei der numerischen Lösung einer Gleichung wichtig, damit sichergestellt ist, dass die numerische Lösung tatsächlich eine Näherungslösung der Gleichung liefert.
Siehe auch
BearbeitenWeblinks
Bearbeiten- The World of mathematical equations. ( vom 7. Juni 2004 im Internet Archive) Umfangreiche englische Seite.
- Equation. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org).
- J. Pahikkala: Equation. In: PlanetMath. (englisch)
- Eric W. Weisstein: Equation. In: MathWorld (englisch).
- The 12 most beautiful equations bbc.com, Archivlink abgerufen am 28. Februar 2022
Einzelnachweise
Bearbeiten- ↑ Robert Recorde: The Whetstone of Witte. London 1557, S. 238.
- ↑ Wolfgang Brauch: Mathematik für Ingenieure / Wolfgang Brauch ; Hans-Joachim Dreyer ; Wolfhart Haacke. Unter Mitarb. von Wolfgang Gentzsch. Teubner, Wiesbaden 2006, ISBN 3-8351-0073-4, S. 40.
- ↑ Hauptseite Gleichungen. Landesbildungsserver Baden-Württemberg, archiviert vom (nicht mehr online verfügbar) am 22. Mai 2015; abgerufen am 8. März 2011.
- ↑ a b Michaela Gruber: Ingenieurmathematik I. Hochschule Landshut, 10. Januar 2017, abgerufen am 1. Februar 2023.
- ↑ Gleichungen. In: Mathematik.net. Abgerufen am 1. Februar 2023.





