Großkreis

Ein Großkreis ist ein größtmöglicher Kreis auf einer Kugeloberfläche. Sein Mittelpunkt fällt immer mit dem Mittelpunkt der Kugel zusammen und ein Schnitt auf dem Großkreis teilt die Kugel in jedem Fall in zwei („gleich große“) Hälften. Da es unendlich viele Möglichkeiten gibt, eine Kugel so zu zerschneiden, dass die Schnittebene den Kugelmittelpunkt trifft, gibt es auch unendlich viele Großkreise.

Großkreis (rot) und Kleinkreis (blau)

Verschiedene Großkreise (durchgezogene Linien). Die gelben Großkreise sind hier Längenkreise. Neigung der 2 schwarzen Großkreise gegen den Äquator (blau) ca. 55° und 60°

Karte in gnomonischer Projektion: Großkreise erscheinen, soweit dargestellt, gerade.

Großkreise spielen z. B. in der Geographie sowie der Schiff- und Luftfahrt eine bedeutende Rolle. Anhand von ihnen werden auch die Zeitzonen festgelegt. Die sphärische Geometrie beinhaltet Großkreise als elementaren Bestandteil. Das Verständnis der Orthodrome als kürzeste Verbindung zweier Punkte auf einer Kugeloberfläche ist unerlässlich für das Verständnis der „geradlinigen“, unbeschleunigten (Abkehr vom Konzept der Gravitation) Bewegung im gekrümmten Raum (allgemeine Relativitätstheorie, Raumkrümmung).

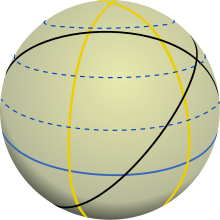
Im geografischen Koordinatensystem der Erde gibt es Sonderfälle von Großkreisen. Sie sind besonders gelagerte Großkreise. Diese Sonderfälle sind der Äquator (hier durchgezogene blaue Linie) sowie die Längenkreise (hier gelbe Linie). Der Äquator ist der Großkreis, der die Erdkugel in der Mitte zwischen Süd- und Nordpol trennt. Die Längenkreise gehen durch den Süd- und durch den Nordpol. Auf ihnen liegen die Meridiane, die sich jeweils vom Nord- zum Südpol erstrecken, wie z. B. der Nullmeridian (0°) und der 180°-Meridian. Die Meridiane werden auch Längengrade genannt. Hingegen sind die Breitenkreise (hier gestrichelte Linien), mit Ausnahme des Äquators, keine Großkreise, sondern kleiner als der maximale Kugelumfang. Man nennt sie deshalb Neben- oder Kleinkreise.

Auf Großkreisen der Erde entspricht eine Bogenminute einer Seemeile, abgekürzt sm (engl. nautical mile, nm oder NM). Sie wird (also als „Längenminute“ bzw. als „Breitenminute am Äquator“) mit 1852 Metern errechenbar bei einem angenommenen Erdumfang von 40.000 km. Der mittlere Erdradius beträgt 6371 km.

Die kürzeste Verbindung zwischen zwei Punkten auf einer Kugeloberfläche – die sogenannte Orthodrome – ist immer Teil eines Großkreises (der sogenannte Hauptbogen). Deshalb führen Schifffahrts- und vor allem Flugrouten meist entlang von Großkreisen. Das Befahren der Erdkugel auf Orthodromen wird Großkreissegeln genannt; bei Start- und Zielpunkt auf ähnlicher geographischer Breite verlaufen die „Großkreiskurse“ dabei über etwas größere Breiten (z. B. München–Peking über Sibirien).

Auf dem Erdellipsoid und anderen Flächen wird die Orthodrome geodätische Linie genannt. Sie ist eine Kurve höherer Ordnung (Abweichung vom Großkreis einer Kugel einige Promille) und entspricht dem Verlauf eines straff gespannten, reibungsfreien Fadens. Auf dem Erdellipsoid, z. B. nach WGS84, berechnet man Anfangskurs und Distanz nach der Formel von Thaddeus Vincenty.

Darstellung auf Karten

Da viele Landkarten (z. B. bei der Mercatorkarte) so dargestellt werden, dass die Breitengrade als gerade, waagrechte Linien erscheinen, wirken die Flugrouten trotz ihrer Kürze gekrümmt und verlaufen weiter polwärts (siehe auch Loxodrome). Um das Zeichnen zu vereinfachen, gibt es spezielle Großkreiskarten (siehe gnomonische Projektion), auf denen alle Großkreise als Gerade erscheinen, die Umgebung allerdings etwas verzerrt ist. Kürzeste Flugrouten und lange kürzeste Schiffsrouten (z. B. bei einer Atlantiküberquerung) können auf einer Gnomonischen Karte als Gerade dargestellt werden. Der dabei zu fahrende Kompasskurs ändert sich dabei stetig und kann auf der Karte abgelesen werden als Winkel zwischen Meridian und Kurslinie.

Auf Seekarten ist am rechten und linken Rand die geografische Breite aufgetragen, d. h. der jeweilige Ausschnitt des betreffenden Längen-Großkreises. Hier kann der Nautiker mit dem Stechzirkel eine Distanz abgreifen (1 Bogenminute = 1 Seemeile = 1,852 km) und zum Einzeichnen von Positionen und Kursen in die Karte übertragen.

Berechnung

Der Winkel zwischen den Punkten $A$ und $B$ mit den Breitenkoordinaten $\varphi$ und den Längenkoordinaten $\lambda$ auf dem Großkreis berechnet sich wie folgt:

$\,\zeta =\arccos {\Big (}\sin(\varphi _{A})\cdot \sin(\varphi _{B})+\cos(\varphi _{A})\cdot \cos(\varphi _{B})\cdot \cos(\lambda _{B}-\lambda _{A}){\Big )}$

Wird $\,\zeta$ im Bogenmaß angegeben, kann die Großkreisentfernung d zwischen den beiden Punkten aus dem Erdradius r_E berechnet werden:

$\,d=\zeta \cdot r_{E}$

Die Großkreisentfernung beträgt maximal den halben Erdumfang.

Den Schnittwinkel des Großkreises von A und B mit dem Meridian im Punkt A nennt man Kurswinkel $\,\omega$. Er berechnet sich mit:

$\cos \omega ={\frac {\sin \varphi _{B}-\sin \varphi _{A}\cdot \cos \zeta }{\cos \varphi _{A}\cdot \sin \zeta }}$

Für östliche Kurse (λ_B > λ_A) liegt der Kurswinkel zwischen 0° und 180°, für westliche Kurse (λ_B < λ_A) liegt der Kurswinkel zwischen 180° und 360°. Im Gegensatz zur ebenen Geometrie unterscheiden sich die Kurswinkel von $A$ nach $B$ und von $B$ nach $A$ nicht um 180°. Im Extremfall, wenn der Großkreis über die Pole führt, können die beiden Kurswinkel sogar gleich sein.

Literatur

• Manfred Leppig: Analytische Geometrie der Großkreise und Loxodromen. 1970.

Weblinks

Wiktionary: Großkreis – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Astronomische Navigation – mit Formeln zum sphärisch-astronomischen Grunddreieck
• Orthodrome (Großkreis)
• Great Circle Mapper – Great Circle mapper including ETOPS ranges (englisch)
• Großkreisberechner
• Ausführliche Großkreisberechnung für die Praxis (englisch)