Job Shop Scheduling
Job Shop Scheduling oder das Job Shop Scheduling Problem (JSP) ist ein Optimierungsproblem mit Anwendungen in der Maschinenbelegungsplanung mit dem Produktionssysteme mit Werkstattfertigung modelliert werden können. Die Aufgabe besteht darin, Aufträge (auch Jobs) optimal auf Maschinen zu verteilen, wobei jeder Auftrag aus verschiedenen Arbeitsschritten besteht, die auf bestimmten Maschinen bearbeitet werden müssen. Dabei kann jeder Auftrag grundsätzlich auch mehrmals auf derselben Maschine bearbeitet werden oder auch manche Maschinen auslassen.
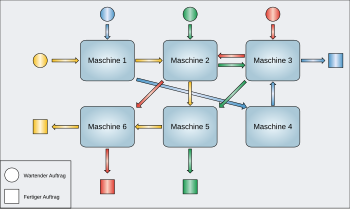
Formulierung als Optimierungsmodell
BearbeitenEs gibt verschiedene Möglichkeiten, das Job Shop Scheduling Problem als gemischt-ganzzahliges lineares Optimierungsproblem (MILP) zu formulieren. Vorgestellt wird das folgendeOptimierungsmodell, welches als disjunctive JSP formulation bezeichnet wird und sich laut Literatur im Vergleich zu anderen Modellen als vorteilhaft erwiesen hat.[1]
Notation
BearbeitenEs seien die Menge der zu verteilenden Jobs und die Menge der zur Verfügung stehenden Maschinen. Für jeden Job sei die Reihenfolge der Maschinen, welche durch die Abarbeitung der Arbeitsschritte benötigt werden. Beispielsweise würde bedeuten, dass Job Nr. 7 aus drei Arbeitsschritten besteht, die zunächst auf Maschine 2 und anschließend auf den Maschinen 1 und 3 erfolgen. Die benötigte Arbeitszeit für Arbeitsschritt auf Maschine wird mit bezeichnet.
Entscheidungsvariablen
BearbeitenDie kontinuierliche Entscheidungssvariable gibt den Startzeitpunkt des Jobs auf Maschine an und die binäre Variable modelliert, ob Job vor Job auf Maschine durchgeführt wird ( ) oder nicht ( ).
Zielfunktion
BearbeitenDie zu minimierende Zielfunktion ist die gesamte Produktionsdauer (auch makespan), d. h. die Dauer zwischen Produktionsbeginn und dem Ende des letzten Bearbeitungsvorgangs.
Nebenbedingungen
Bearbeiten- Zunächst wird durch die Nebenbedingung für alle Jobs und Maschinen sichergestellt, dass innerhalb eines Jobs die Reihenfolge der Arbeitsschritte eingehalten wird.
- Die Restriktionen und für alle mit sowie alle garantieren, dass nicht zwei Jobs gleichzeitig auf derselben Maschine durchgeführt werden können. Dabei ist das eine Zahl, die ausreichend groß gewählt werden sollte. Eine mögliche Wahl ist . Die Variable aktiviert und deaktiviert also mit Hilfe der großen Zahl jeweils eine der beiden Ungleichungen, was als Big-M-Formulierung bezeichnet wird.[2]
- Letztlich gilt für die Produktionsdauer für alle Jobs .
Lösungsmethoden
BearbeitenDas oben vorgestellte Optimierungsmodell kann für kleine bis mittlere Problemgrößen (bis etwa 30 Jobs und 30 Maschinen) exakt mit Hilfe von Branch-and-Bound-Methoden gelöst werden, die in Solvern wie CPLEX, Gurobi oder SCIP implementiert sind.[1] Außerdem eignen sich Constraint Programming Methoden und auf Scheduling spezialisierte Verfahren wie das iSTS-SGS[3] für die Lösung moderater Instanzen. Für größere Probleminstanzen werden Metaheuristiken und problemspezifische Heuristiken, die gute Konfigurationen berechnen, ohne eine Aussage bezüglich deren globaler Optimalität zu treffen.
Varianten
BearbeitenWenn die Folge der Arbeitsgänge für jeden Auftrag identisch ist, handelt es sich um einen Flow-Shop, der ein Modell der Fließproduktion darstellt. Wird auf jeder Maschine die gleiche Folge von Aufträgen bearbeitet, handelt es sich um einen Permutations-Job Shop. Für den Fall, dass nur eine Maschine vorhanden ist, ergibt sich ein Ein-Maschinen Problem; falls die Aufträge aus nur einem Arbeitsgang bestehen, der auf einer beliebigen Maschine zu bearbeiten ist, handelt es sich um ein Maschinenbelegungsproblem mit parallelen Maschinen.
Siehe auch
BearbeitenLiteratur
Bearbeiten- Jacek Blazewicz et al.: Handbook on Scheduling. 2. Auflage, Springer, Berlin, Heidelberg, 2019, ISBN 978-3-319-99848-0.
- Wolfgang Domschke, Armin Scholl, Stefan Voß: Produktionsplanung: Ablauforganisatorische Aspekte. 2. Auflage, Springer, Berlin, Heidelberg 1997, ISBN 3-5406-3560-2.
- Michael L. Pinedo: Scheduling. 4. Auflage, Springer, Berlin, Heidelberg, 2012, ISBN 978-1-4899-9043-3.
Einzelnachweise
Bearbeiten- ↑ a b Wen-Yang Ku, J. Christopher Beck: Mixed Integer Programming models for job shop scheduling: A computational analysis. In: Computers & Operations Research. Band 73, September 2016, ISSN 0305-0548, S. 165–173, doi:10.1016/j.cor.2016.04.006 (utoronto.ca [PDF; abgerufen am 18. Januar 2024]).
- ↑ Nathan Sudermann-Merx: Einführung in Optimierungsmodelle. 2023, doi:10.1007/978-3-662-67381-2 (springer.com [abgerufen am 19. Januar 2024]).
- ↑ J. Christopher Beck, T. K. Feng, Jean-Paul Watson: Combining Constraint Programming and Local Search for Job-Shop Scheduling. In: INFORMS Journal on Computing. Band 23, Nr. 1, Februar 2011, ISSN 1091-9856, S. 1–14, doi:10.1287/ijoc.1100.0388.

