Periodogramm
Das Periodogramm ist ein Schätzer für die spektrale Leistungsdichte eines Signals. Gesucht ist also eine Funktion , welche die Verteilung der Leistung (oder Energie) des Signals auf die Kreisfrequenz angibt. Der Ausdruck wurde von Arthur Schuster 1898 geprägt.[1] Die Methode wird eingesetzt in der Signalverarbeitung, Elektrotechnik, Physik und Ökonometrie. Ein wichtiges Beispiel sind Spektrum-Analysatoren.
Im mathematischen Sinn ist das Periodogramm ein nicht konsistenter Schätzer, siehe auch Spektraldichteschätzung.
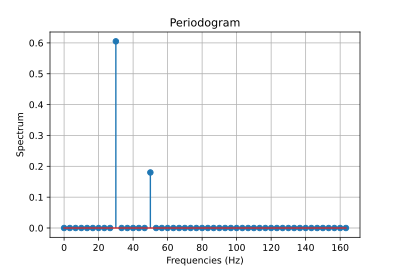
Kontext und Konventionen
BearbeitenIn der Regel sind nur Abtastwerte des Signals zu diskreten Zeitpunkten mit konstanter Abtastdauer gegeben, und man beschränkt sich zur Abschätzung auf Abtastwerte, z. B. mit , d. h. auf ein Zeitintervall der Dauer .
Ein wesentlicher Schritt des Verfahrens ist eine diskrete Fourier-Transformation. Die Einschränkung der Fourier-Transformation auf ein Zeitintervall der Dauer lässt sich erreichen durch Multiplikation des Signals mit einer Fensterfunktion . Im einfachsten Fall ist eine Rechteckfunktion der Breite .
Um Artefakte im Spektrum (aufgrund der Unstetigkeiten des Rechteckfensters) zu verringern, werden jedoch in der Regel Fenster mit langsameren Änderungen und eigenen Bezeichnungen verwendet, z. B. das Parzen-Fenster oder das „Welch-Fenster“. Man spricht dann von einem modifizierten Periodogramm.[2]
Für die diskrete Fouriertransformierte des Signals wird die Schreibweise verwendet. Hierbei sind nur Kreisfrequenzen mit zulässig.
Definition
BearbeitenDas Periodogramm ist definiert gemäß
In Übereinstimmung mit dem Abtasttheorem ist das Periodogramm -periodisch. Man beschränkt sich daher auf ein Intervall (Brillouin-Zone) oder .
Den Normierungsfaktor betreffend gibt es verschiedene Konventionen. Eine wichtige Kenngröße hierbei ist das mittlere Amplitudenquadrat (die mittlere Leistung) des Signals. Die Normierung ist so gewählt, dass der Mittelwert von bestmöglich mit übereinstimmt.
Falls die Amplitude des Signals digitalisiert ist und Maximalwert hat, ist das Periodogramm auch relativ zum Maximum normierbar (Fullscale). Das Maximum wird für monochromatische Signale erreicht, das Full-Scale Periodogramm ist
Beispiele
BearbeitenWeißes Rauschen
BearbeitenEs sei ein weißes Rauschen mit Varianz , . Das Ensemble-Mittel des Betragsquadrats der Fourier-Transformierten ist dann
Das Periodogramm hat den Mittelwert , und zwar unabhängig von der Fensterlänge. Alle Frequenzen geben denselben Energiebeitrag.
Konstantes Signal
BearbeitenFür den Frequenz-Mittelwert von lassen sich allgemeine Aussagen machen. Ausgangspunkt ist
Für konstantes Signal wird
Der Mittelwert des Periodogramms ist (unabhängig von ) ebenfalls . Das Periodogramm liefert bei konstantem Signal einen Peak bei Frequenz . Mit wachsendem wird dieser Peak höher und schmäler.
Rechteck-Fenster
BearbeitenIm Fall eines Rechteck-Fensters gilt die Parseval-Gleichung . Durch Division durch folgt der Mittelwert des Periodogramms . Dieser Wert ist von unabhängig, sofern dies für das mittlere Amplitudenquadrat gilt.
Einschränkungen und Verbesserungen
BearbeitenDie Zahl der Werte im Periodogramm wächst mit der Fensterlänge , die Werte werden dabei jedoch nicht genauer. Im Fall eines weißen Rauschens mit Amplitude bleibt die Varianz der Periodogramm-Werte bei wachsender Fensterlänge von der Größenordnung .[3] Abhilfe schafft eine Mittelung benachbarter Werte oder eine Mittelung über mehrere Periodogramme.[2]
Kontinuierliches Signal
BearbeitenFür ein auf dem Zeit-Kontinuum definiertes Signal ist die Fourier-Transformierte des Produktes von Signal und Fensterfunktion
Das Periodogramm ist
Wie beim abgetasteten Signal bleibt die Standardabweichung der Periodogramm-Werte bei wachsender Zeitreihenlänge im ungünstigsten Fall von derselben Größenordnung wie die Werte selber.
Einzelnachweise
Bearbeiten- ↑ Arthur Schuster: On the investigation of hidden periodicities with application to a supposed 26 day period of meteorological phenomena, Terrestrial Magnetism and Atmospheric Electricity, 3, S. 13–41, 1898
- ↑ a b William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery, Michael Metcalf: Numerical Recipes in C, Cambridge University Press, 1992, ISBN 0-521-43108-5
- ↑ Monson H. Hayes: Statistical Digital Signal Processing and Modeling, John Wiley & sons, inc, 1996, ISBN 978-0-471-59431-4

