Satz von Donsker

Der Satz von Donsker ist ein fundamentaler Satz aus der Stochastik, genauer aus der Theorie der stochastischen Prozesse. Er ist die funktionale Variante des zentralen Grenzwertsatzes und ist deshalb auch unter dem Namen Funktionaler Grenzwertsatz und Donskersches Invarianzprinzip bekannt.

Donskersches Invarianzprinzip für die einfache Irrfahrt auf den ganzen Zahlen $\mathbb {Z}$.

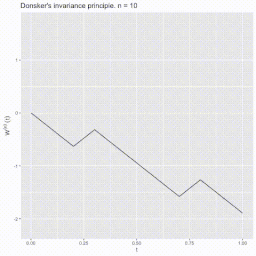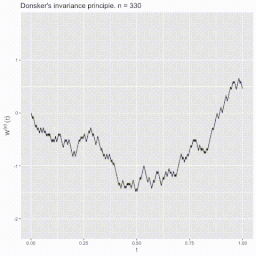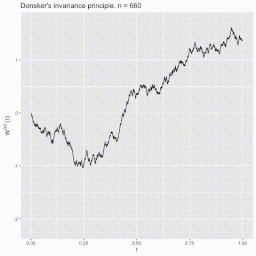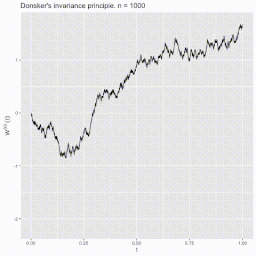
Der Satz begründet die Existenz des Wiener-Maßes bzw. der Brownschen Bewegung. Er bietet zugleich eine Konstruktionsmöglichkeit mittels Zufallsvariablen im Skorochod-Raum ${\mathcal {D}}[0,1]$. Der Satz wurde 1952 vom amerikanischen Mathematiker Monroe D. Donsker bewiesen.

Aussage

Seien $C[0,1]$ der Raum der reellen stetigen Funktionen auf dem Intervall $[0,1]$ und ${\mathcal {B}}(C[0,1])$ die borelsche σ-Algebra auf $C[0,1]$. Weiter seien $(\Omega ,{\mathcal {F}},P)$ ein Wahrscheinlichkeitsraum und $(X_{n})_{n\in \mathbb {N} }$ unabhängig und identisch verteilte reellwertige Zufallsvariablen darauf, sodass $\mathbb {E} [X_{n}]=0$ und $\mathbb {E} [X_{n}^{2}]=\sigma ^{2}$ für alle $n\in \mathbb {N}$ gilt. Betrachte die Irrfahrt ${\textstyle S_{n}=\sum _{k=1}^{n}X_{k}}$ mit $S_{0}=0$ und konstruiere die Zufallsvariable $$X_{t}^{(n)}(\omega )=({\sqrt {n}}\sigma )^{-1}\left(S_{[nt]}(\omega )+(nt-[nt])X_{[nt]+1}(\omega )\right)$$für $t\in [0,1]$, wobei $[x]$ die Abrundungsfunktion darstellt. Die Zufallsvariable $X_{\cdot }^{(n)}\colon \Omega \to C[0,1]$ ist die stückweise lineare Interpolation der Irrfahrt mit diskreten Punkten ${\textstyle X_{i/n}^{(n)}(\omega )=(\sigma {\sqrt {n}})^{-1}S_{i}(\omega )}$ für $i\in \{0,\dots ,n\}$.

Sei nun ${\mathcal {M}}$ der Raum der Wahrscheinlichkeitsmaße auf $(C[0,1],{\mathcal {B}}(C[0,1]))$ und bezeichne mit $\mu _{n}\in {\mathcal {M}}$ das Bildmaß $\mu _{n}=P\circ (X_{\cdot }^{(n)})^{-1}$. Dann konvergiert $\mu _{n}$ schwach gegen das Wiener-Maß, wenn $n\to \infty$. Mit anderen Worten konvergiert $X_{\cdot }^{(n)}$ in Verteilung gegen einen Standard-Wiener-Prozess $W_{\cdot }$, wenn $n\to \infty$.

Erläuterungen

• Da der Satz keine zugrundeliegende Verteilung an die $X_{n}$ voraussetzt (nur dass diese unabhängig und identisch verteilte Zufallsvariablen sind), spricht man vom Donskerschen Invarianzprinzip.