Stapelfehler
Ein Stapelfehler ist ein 2-dimensionaler Gitterfehler in bestimmten Kristallstrukturen. Der Fehler tritt im Allgemeinen in den dichtest gepackten Kristallebenen der kubisch dichtesten Kugelpackung (kdP) oder der hexagonal dichtesten Kugelpackung auf, weil hier die Wechselwirkung zwischen den Atomen am stärksten ist. Ein Stapelfehler liegt vor, wenn die Stapelung der Kristallebenen, z. B. die Abfolge -A-B-C-A-B-C-, in ihrer Regelmäßigkeit unterbrochen wird.
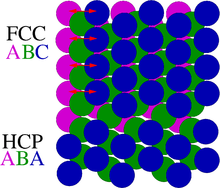
Stapelfehler in verschiedenen Kristallsystemen
BearbeitenKubisch-flächenzentriertes Kristallsystem
BearbeitenIn der kdP bzw. einer kubisch flächenzentrierten Struktur (engl. FCC) sind die {111}-Ebenen am dichtesten, die in <111>-Richtung gestapelt werden. Sie können als Abfolge -A-B-C-A-B-C- dargestellt werden.
Es existieren zwei mögliche fehlerhafte Stapelfolgen:
- ein extrinsischer Stapelfehler wird durch eine hinzugefügte Ebene dargestellt, z. B. -A-B-A-C-A-B-C-.
- ein intrinsischer Stapelfehler ist entsprechend das Fehlen einer Ebene, z. B. -A-B-C-B-C-A-B-C-.
Üblicherweise bildet sich bei der kfz-Struktur eine lokale hexagonale Gitterstruktur (engl. HCP) mit der Stapelung -A-B-C-A-B-C- aus. Diese Periodizität entsteht auch, wenn ein Kristallteil um den unvollständigen Gittervektor a/6 <112> verschoben wird (a ist die Kantenlänge der Elementarzelle). Durch die Verschiebung werden die A-Ebenen zu B-Ebenen, die B-Ebenen zu C-Ebenen und die C-Ebenen zu A-Ebenen.[1]
Hexagonales Kristallsystem
BearbeitenIn der hdP bzw. einer hexagonalen Gitterstruktur sind die {0001}-Ebenen am dichtesten, die in <0001>-Richtung gestapelt werden. Hier ist jede zweite Netzebene identisch, -A-B-A-B-.
- Der extrinsische Fehler ist entsprechend -A-B-C-A-B-C-.
- Das Fehlen einer Stapelebene gibt es hingegen nicht, weil sonst zwei gleiche Ebenen übereinander liegen würden und nicht mehr dichtest gepackt sein könnten. Ein intrinsischer Stapelfehler ist nur möglich durch die Verschiebung eines Kristallteils um den Gittervektor a/3 in Richtung <21-20>, bei der B-Ebenen zu C-Ebenen und A-Ebenen zu B-Ebenen werden, -A-B-C-A-C-A-.
Kubisch-raumzentriertes Kristallsystem
BearbeitenObwohl in kubisch raumzentrierten Strukturen (krz) keine dichteste Packung vorliegt, kann eine Stapelung von {211}-Ebenen angenommen werden. Daraus würde eine Periode mit 6 Ebenen folgen: -A-B-C-D-E-F-. Diese Metalle besitzen meist eine hohe Stapelfehlerenergie, weshalb ausgedehnte Stapelfehler selten von Bedeutung sind.
Bedeutung und Messung
Bearbeiten| Metall | SFE (mJ m−2) |
|---|---|
| Bronze | <10[2] |
| Stahl | <10[2] |
| Ag (Silber) | 20–25[1][2] |
| Si (Silicium) | >42 |
| Cu (Kupfer) | 60[1] -78[3][4], 100[5] |
| Au (Gold) | 10[5], 75[2] |
| Mg (Magnesium) | 125[6] |
| Fe (Eisen) | 140 ± 40[7] |
| Ni (Nickel) | 90[2][8] - 300[1] |
| Al (Aluminium) | 160–250[9][2] |
| Zn (Zink) | 250[1] |
Der Stapelfehler ist ein wichtiger Gitterfehler, da er zur Bildung von Korngrenzen führt und so die Bildung von Einkristallen verhindert.
Stapelfehler entstehen z. B. durch Zwillingsbildung oder wenn eine Partialversetzung durch den Kristall läuft. Je kleiner die dazu nötige Stapelfehlerenergie (SFE, stacking fault energy), desto leichter bildet sich ein Stapelfehler. Versetzungen können sich deshalb leicht in Partialversetzungen aufspalten. Schraubenversetzungen müssen dann zum Quergleiten unter Energieaufwand wieder einschnüren, deswegen steigt die Festigkeit.
Die Aufspaltungsweite spielt weiterhin eine wichtige Rolle bei der Warmumformung. Da aufgespaltene Versetzungen schlecht quergleiten oder klettern können, ist bei Werkstoffen mit geringer Stapelfehlerenergie die dynamische Kristallerholung behindert und es findet eine stärkere Verfestigung des Metalls statt. Es kann sich so eine genügend große treibende Kraft für dynamische Rekristallisation aufbauen, die zu einem Kraftmaximum in der Warmfließkurve führt.
Bei austenitischen Stählen sinkt die Stapelfehlerenergie im Gegensatz zu reinem Eisen z. T. deutlich ab und zeigt deshalb einen TWIP-Effekt.
Einzelnachweise
Bearbeiten- ↑ a b c d e Oettel, Heinrich, Schumann, Hermann: Metallografie mit einer Einführung in die Keramografie. 15., überarb. und erw. Auflage. Weinheim, ISBN 978-3-527-32257-2, S. 47.
- ↑ a b c d e f Richard W. Hertzberg, Richard P. Vinci, Jason L. Hertzberg: Deformation and Fracture Mechanics of Engineering Materials. John Wiley & Sons, Inc, 2013, ISBN 978-0-470-52780-1, S. 80.
- ↑ Venables, J. A. (1964). The electron microscopy of deformation twinning. Journal of physics and chemistry solids, 25, 685–690.
- ↑ Zhao, Y.H., Liao, Y.Y., Zhu, Y.T. (2005). Influence of stacking fault energy on nanostructure under high pressure torsion. Materials Science and Engineering A, 410–411, 188–193.
- ↑ a b Erhard Hornbogen, Gunther Eggeler, Ewald Werner: Werkstoffe (= Springer-Lehrbuch). Springer Berlin Heidelberg, Berlin, Heidelberg 2008, ISBN 978-3-540-71857-4, S. 67, doi:10.1007/978-3-540-71858-1 (springer.com [abgerufen am 5. Januar 2022]).
- ↑ N.V. Ravi Kumar et al., Grain refinement in AZ91 magnesium alloy during thermomechanical processing, Materials and Engineering A359 (2003), 150–157.
- ↑ Hermann Schumann: Einfluß der Stapelfehlerenergie auf den kristallographischen Umgitterungsmechanismus der γ/α-Umwandlung in hochlegierten Stählen. In: Kristall und Technik, Jg. 9 (1974), Heft 10, S. 1141–1152, ISSN 0023-4753 doi:10.1002/crat.19740091009.
- ↑ Luc Remy. PhD thesis, Universite de Paris-Sud, Orsay, France, 1975.
- ↑ Lawrence E. Murr. Interfacial Phenomena in Metals and Alloys. Addison-Wesley Pub. Co., 1975.